Chapter 1, An Introduction to Information Retrieval

Information Retrieval is a broad term that can be summarized as “taking thing(s) that fullfill criteria(s) from collection”. Even deciding which cereal box your cousin will like most for his 6th birthday party breakfast can be considered as a form of IR; however as an actual academic field of study its more formal definition is:

“The act of finding material (usually documents) of an unstructured nature (usually text) that satisfies an information need from within large collections (usually stored on computers)”

The most visible aplication for this field can be seen at Web Search Engine such as Bing, Yahoo, Baidu, AOL, Ask, and Lycos.

The way this sites work is fairly simple to understand yet hard to implements:

1. The sites ask for “the criteria(s)” of the webpage we want in form of a Query.
2. It then proceeds to traverse “the collection” of webpages, and give each one “relevance point” on how well this webpage fullfill the given Query
3. Finally, the sites display the result in form of a list of page with the most relevant page on top, descending according to relevance or likeliness to the query.

Due to the unstructured nature of a webpage / documents in general, it would be very difficult for a system to process a user query on every documents raw form. That is why IR system usually pre-process each document into a suitable model first; think of it as the documents cover, it gives the system a sense of what the sites contain without needing to read the whole thing.

There are all sort of model already developed for IR system, each whith its own query format, advantages, and disadvantages. One of such model which we will elaborate later is The Extended Boolean Model.

Chapter 2, The Standard Boolean Model

As the name would imply, Extended Boolean Model is an Extended version of the Standard Boolean Model. So it might be good to try to understand the basic of Boolean Model first before going ahead (still, there’re not that much similarities between them, so feel free to skip this chapter if you wish). Basically this particular IR model works by storing the information of a document content in form of a list containing words/terms that exist in said document. For example, consider the following picture:

The matrix above is used to store a boolean model of six documents. From there, we can clearly see what terms d1 contained. Or, more practically, we can use this matrix to get a list of documents that contain certain terms like “Voyage”, or “Trip” during certain queries.

You might notice that there are only five terms that are listed above. Articles usually have many more words inside them, even though most of them are not really that important at reflecting the article’s content, so why are there only five words listed above? This is because a concept most IR system use called Indexing.

Certain words like “is”, “and”, and “not” not important when trying to figure out what is an article about, and can be safely omited to safe space and processing time; this concept is called indexing. A couple of “technique” that can be used to achieve this are as follow:

• Manually supply a list of words that can be safely omited, and skip these words while creating the documents model
• Ignore word with a fairly low, or high, use rate in a document. Statistically these words have the lowest chance to reflect the documents content, so they should be safe to be ignored.

On to the next topic; Query of a boolean model is expressed in form of a boolean expression (using operator AND ,OR, and NOT) about terms that’s required to be present(or not) at the results. During query processing, there are only 2 posible relevance point for this model: satisfy the query and not satisfy the query. Naturally, only the satisfying one will be shown at the final result.

For example, using the picture above, query “voyage AND trip” would return the intersection of voyage array and trip array, resulting in array 000100, which mean that only the 4th document met that query criteria. The query ((NOT voyage) OR ocean) would return the union of ocean array and the complement of voyage array, resulting in 000000, which mean that none of the documents match the query. Simple.

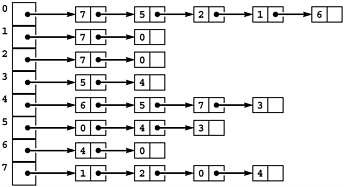
In the implementation of the Boolean Model, it is common practice to have an indexed lists containing terms/words in the vocabullary, and on each one have a list of documents ID that contains such terms. So processing a query can be summarized as:

1. X AND Y, return document IDs that occur in both X list and Y list
2. X OR Y, return document IDs that occur in either X list or Y list
3. NOT X, return document IDs that do not occur in X list
4. (X AND (NOT Y)) OR Z, return document IDs that occur in either Z list or IDs that occur in X list but not in Y

And that is the basic of the standard Boolean Model, it is fairly easy to implement and understand but not without its weaknesses:

• With only 2 possible relevance point, there are no way to rank documents in order of relevance.
  • The model only concern itself with wether or not a term exist, not it’s frequency of use and relevance in the document.
  • A user might find the term he/she wants only mentioned once in one of the query result and not that relevant in said document
• There are some results which might be counterintuitive to user due to this model strict use of boolean operator.
  • For example the query W AND X AND Y AND Z, will not result in a document which contain the term W, X, and Y; even though the user might be interested in this document if no others fullfill this query.
  • Also, in the query A OR B OR C, a document which mention only A is considered as important as a document mentioning all terms.
• There are no way to assign importance factor to parts of query, which my be desired by advanced user.

Which is why several models had been proposed to improve upon this basic model, with an attempt to address the issues above…

Chapter 3, The Extended Boolean Model

The Extended Boolean Model is really just a general term that refer to all IR model that improve upon the Standard Boolean Model. There had been proposed many such model, such as the MMM model, the Paice model and P-norm model. This article will mainly focus its discussion around the P-Norm model (the more feature complete out of the three), and if interested, the explanation of the other model (as well as this article source) can be found here:

Extended Boolean Model by E. Fox, S. Betrabet, M. Koushik and W. Lee

The concept of the P-Norm model is similar to its predecessor, but it made some changes into it; adding more features and capability. One of the most important changes are the addition of term weights for every term appearance in a document. This concept is called term weighting, it is basically a way to measure and note how relevant is a term in a document.

For example, in this article, the term “Query” should receive a higher score than the term “voyage”. Even though both of them appeared, the term “Query” is more relevant in this document; it can be seen from the fact that the term “Query” is mentioned way more often than “voyage”. There are all sort of way to weight terms. One of them, namely the TF-IDF, take these factors into account:

1. How often is the term used in the document.
2. How long is the document.
3. How many other document use the same term.

And transform these idea into a simple yet effective term weighting formula:

• TF(t) = (Number of Times Term t Appears) / (Total Number of Terms)
• IDF(t) = log_e(Total Number of Documents / Number of Documents with Term t in it)
• TF.IDF(t) = TF(t) x IDF(t)

With this formula (or using other method you prefer), each term appearance in a document can be given an appropriate weight. This way, the system can diferentiate between a document that mention the term “voyage” as an example and the one that actually contains voyage advisory content. Moreover, the P-Norm model also allows for term weighting in queries as well. This’ll allow advanced user to gain more spesific documents by using a more spesific query.

With all of these changes, the query processing process must be changed as well. P-Norm had a very different query processing method compared to the Standard Boolean Model. Previously the model can only give a binary result, either a document fullfills the query or it didn’t.

The P-Norm model change this into a formula that resulted in an arbitrary number, which portray the document likeliness to the query. The value of this number vary largely between system depend on the weighting method used on the document and query; but it doesn’t matter since all we need to do is sort the result according to this value. A high likeliness value document should be put above a low one, this way we can rank the result according to how well it fullfill the query. The followings are the formula used in the P-Norm model:

The similarity of query q-and ( “a-1 AND a-2 AND … AND a-t” where a-n is the nth term ) and the document d-j where the weight of term a-n is w-n (if the term doesn’t exist then the weight is 0) is :

It will yield the highest result when the weight of the terms desired is highest (for example w-n = 1), and will decrease as the weight of terms desired get lower.

The similarity of the query q-or (“a-1 OR a-2 OR … OR a-t”) and the document d-j is :

It will yield the lowest result when the weight of the terms desired is lowest (for example w-n = 0), and will increase as the weight of terms desired get higher.

The formula used to calculate the similarity of the query q-not (“not q” where q is a subquery) and the document d-j is :

sim(q-not,dj) = 1 - SIM(q,dj)

With the three basic formulas above, we can easily count the similarity of more complex query; for example, The similarity formula between q = “(a-1 AND a-2) OR a-3” is:

Observe that the sub-query “a1 AND a2” is treated as a term weight, this concept will prove usefull during implementation

As briefly mentioned above, the P-Norm method also enable term weighting in query. This can be achieved by slightly alter the formula above to consider the query term weight. To calculate the similarity of the query q = “a-1 k-1 AND/OR a-2 k-2 AND/OR … a-n k-n” (k-n is the n-th term and a-n is the weight of term k-n) and the document D where the weight of term k-n is da-n, are as such:

And with that, we can now easily calculate the similarities between any boolean query and a documents model. Additional notes:

• The p used in the formulas above is called the degree of strictness, usually implemented as a system defined constant like 2. At p-value of 1, both q-or and q-and will yield the same result.
• When t=1 (a query with only one term), both q-and and q-or provide in the same result, SIM(q,dj) = w1

Chapter 4, Implementation

Implementation of the Extended Boolean Model can be done in many different ways. Below is one of the common way of doing things:

• Document Model Implementation:
  • Rather than imitate the Standard Boolean model and have a list of terms each containing document id of all the documents that contains such term, it is better to do the opposite.
  • Because query processing will be done per-document it will make more sense to create a list of document each containing list of term ids of terms that contained within.
  • This way, we can process query sequentially down the document list and see the terms contained within and its weight relative to the document.
• Query Implementation:
  • One the best way to implement a boolean query is to store them in form of an n-ary Tree
  • Each leaf is a term (and it’s weight), and each internal node is the operator linking it’s children together
  • For example, the query ((A OR B OR C) AND (D OR E)) will be represented as:
  • 
  • To read the query from a tree do so by using the Inorder Tree Transversal method
• Query Processing:
  • Query processing can be done recursively by self-call (let’s just call the method Query(Node) for now)
  • Basis, If the node is a leaf node, return the node weight
  • Recurrent:
    • Identify which kind of query this is (AND/OR/NOT),
    • Calculate the weight of every sub-tree below this node by calling Query(Node-i)
    • Return the value of this query tree by using the appropriate formula
  • For example, using the picture above:
    • The process for node AND will call the Query method for both node OR
    • Each node OR will call the Query method for each of their sons, and return the similarity between its subquery and the document
    • The method called to the AND node will return the result of using the qand formula with t=2 where w1 is the result of subquery OR1 and w2 is the result of subquery OR2.
  • This way, document ranking can be done sequentially down the document list by assigning similarity value to each of the document then sorting it from highest similarity to the lowest one.

References

Extended Boolean Model by E. Fox, S. Betrabet, M. Koushik and W. Lee

Term frequency and weighting from Cambridge University Press

Boolean retrieval from Cambridge University Press

Information Retrieval Lecture from The Department of Computer Science

Pictures from Wikipedia Extended Boolean Model Article