Penyelesaian Traveling Salesperson Problem dengan Berbagai Algoritma
Oleh Sri Umay N.S. / 13514007
Apa itu Traveling Salesperson Problem?
Traveling Salesperson Problem (TSP) adalah salah satu permasalahan klasik yang sering dijumpai dalam kehidupan sehari-hari. Permasalahan ini bermula dari permasalahan pedagang keliling yang ingin mengunjungi setiap tempat (misal kota) dari suatu kota awal menuju ke semua kota lain tepat satu kali dan kembali lagi ke kota awal dengan biaya/jarak seminimal mungkin. Permasalah ini merupakan permasalan optimasi yang membutuhkan penyelesaian dengan hasil yang paling optimum berdasarkan permasalah yang dicari solusinya dengan tepat. Contoh nyata dari permasalahan ini adalah suatu sales pabrik yang ingin menawarkan barang di semua kota di provinsi Jawa Timurd dengan menaiki truk. Untuk mengefisienkan bahan bakar dan ongkos perjalanan, maka sales perlu menemukan rute dimana ia dapat mengunjungi semua kota di Jawa Timur dengan jarak sesingkat mungkin. Ketepatan penyelesaian tersebut sangat mempengaruhi tujuan dari dicarinya solusi masalah. Jadi dalam permasalahan ini bukanlah tentang soluusi mana yang benar dan salah, melainkan solusi mana yang lebih optimal.
Bagaimana Cara Penyelesaiannya?
Persoalan TSP biasa dimodelkan dengan sebuah graf, dengan simpul pada graf merepresentasikan kota dan sisi graf yang merepresentasikan jarak antar kota atau biaya yang diperlukan untuk berpidah dari suatu kota ke kota lain tergantung dengan apa persoalan optimasi yang diingikan.
Penyelesaian masalah ini sering dirumuskan dengan pendekatan komputasi dengan menggunakan berbagai algoritma karena cukup kompleks. TSP merupakan salah satu permasalah yang dikategoritan dalam permasalahan NP dan masih diperdebatkan apakah masuk kedalam NP-hard atau NP-complete.
Untuk menyelesaikan TSP ada berbagai algoritma yang dapat digunakan, antara lain :
-
[Algoritma Brute Force] (#alg_bruteforce)
-
[Algoritma Greedy] (#alg_greedy)
-
[Algoritma Branch and Bound] (#alg_bnb)
-
[Dynamic Programming] (#alg_dprog)
Untuk lebih mudah memahami persoalan TSP ini, berikut adala contoh persoalan TSP sederhana yang akan diselesaiakan dengan algoritma yang telah disebutkan diatas.
Contoh Persoalan TSP
(Sumber gambar : https://upload.wikimedia.org/wikipedia/commons/3/30/Weighted_K4.svg)
Graf seperti pada gambar diatas adalah contoh pemodelan TSP dengan graf. Pada graf diatas dimisalkan simpul adalah kota dan nama simpul graf adalah nama kota, sementara sisi pada graf adalah jarak antar satu kota ke kota lain. Persoalannya, seorang pedagang keliling ingin menawarkan dagangannya ke semua kota, yaitu kota A, B, C, dan D. Untuk meminimalkan biaya perjalanan, pedangang keliling tersebut ingin mengetahui rute yang menghubungkan keempat kota tersebut, dimulai dari kota A, mengunjungi kota B, C, dan D tepat sekali kemudian kembali ke kota A, yang memiliki panjang rute paling pendek sehingga bahan bakar untuk menempuh perjalanan juga menjadi lebih hemat. Rute manakah yang merupakan rute terpendek?
Berikut adalah penjelasan algoritma untuk penyelesaian persoalan TSP diatas.
1. Algoritma Brute Force
Algoritma brute force adalah algoritma dengan implementasi paling sederhana. Penyelesaian dengan algoritma brute force dilakukan dengan cara mengenumerasi semua kemungkinan jalur yang dapat ditempuh dari simpul awal untuk mengunjungi setiap simpul tepat satu kali dan kembali ke simpul awal, setelah itu dicari jalur mana yang menghasilkan total bobot dengan nilai optimum (optimum yang dimaksud adalah berdasarkan spesifikasi ynag diinginkan, biasanya nilai terbesar atau terkecil).
Penyelesaian denga cara ini sangatlah mahal karena harus mengenumerasi semua kemungkinan yang bahkan kemungkinan terburuk sekalipun, sehingga untuk n buah simpul (kota), kemungkinan jalur yang dienumerasi bisa mencapai n! jalur, sehingga kompleksitas untuk menyelesaikan TSP dengan algoritma brute force ini bernilai faktorial atau O(n!). Tentu penyelesaian persoalan TSP dengan algoritma brute force bukanlah ide yang baik karena kompleksitasnya sangat besar. Misal untuk menyelesaikan permasalan TSP dengan n buah kabupaten/kota di Jawa Timur saja, yaitu 29 kabupaten dan 9 kota, kompleksitas programnya menjadi luar biasa besar dan sangat tidak efisien. Namun untuk menyelesaikan permasalahan sederhana seperti contoh persoalan diatas yang hanya terdiri dari 4 kota, penyelesaian dengan algortima brute force masih sangat mungkin untuk dilakukan.
Berikut adalah langkah penyelesaiannya. * #### Enumerasi seluruh kemungkinan jalur Langkah pertama yang dari penyelesaian dengan cara brute force adalah mengenumerasi semuan kemungkinan jalur pada graf yang dimulai dari simpul A, melewati seluruh kota selain A tepat sekali, dan kembali ke A. Selain mengenumerasi setiap jalur, jarak total dari jalur tersebut juga dihitung untuk menentukan jalur mana yang paling optimal, jarak total seluruh jalur akan dibandingkan.
| Jalur yang mungkin | Perhitungan Jarak | Jarak total |
|---|---|---|
| A > B > C > D > A | 20 + 30 + 12 + 35 | 97 |
| A > B > D > C > A | 20 + 34 + 12 + 42 | 108 |
| A > C > B > D > A | 42 + 30 + 34 + 35 | 151 |
| A > C > D > B > A | 42 + 12 + 34 + 20 | 108 |
| A > D > B > C > A | 35 + 34 + 30 + 42 | 151 |
| A > D > C > B > A | 35 + 12 + 30 + 20 | 97 |
-
Cari jalur dengan jarak total terkecil
Setelah diketahui seluruh jalur yang mungkin beserta jaraknya, maka tinggal mencari jalur mana yang memiliki jarak paling kecil diantara semua jalur. Setelah ditemukan jalur dengan jarak terkecil, maka jalur tersebut adalah jalur yang merupakan solusi persoalan TSP di atas.
Untuk persoalan di atas, dari tabel dapat dilihat bahwa jalur dengan jarak terkecil adalah jalur A>B>C>D>A dan A>D>C>B>A, maka kedua jalur tersebut adalah solusi dari persoalan.
2. Algoritma Greedy
Selain algoritma brute force, algoritma greedy merupakan salah satu algortima yang dapat digunakan untuk mencari solusi dari persoalan TSP. Sama seperti namanya ‘greedy’, cara kerja algoritma ini adalah dengan mecari ‘solusi’ terbaik di setiap langkahnya tanpa memikirkan apakah langkah yang diambil tersebut akan benar-benar menghasilkan solusi yang optimal secara keseluruhan kelak. Dengan menggunakan algoritma greedy ini, komplesitas algortima untuk menyelesaikan persoalan TSP ini dapat di reduksi dengan kompleksitasnya menjadi polinomial saja, namun permasalah dari algoritma ini adalah tidak selalu memberikan solusi yang tetap atau yang paling optimal. Seperti yang telah dikatakan diatas, algoritma ini menitikberatkan pada kemungkinan ‘solusi’ jangka pendek yang paling optimal, namun solusi keseluruhannya tidak dapat dijamin optimal. Justru seringkali bukanlah solusi yang optimal. Sehingga meski kompleksitanya sangat kecil, algoritma ini tidak benar-benar dapa digunakan untuk menyelesaikan persoalan ini. Namun sebagai perbandingan, algoritma ini cukup untuk memperkirakan solusi yang ‘mendekati’ optimum mengingat kompleksitasnya yang kecil.
Misal untuk menyelesaikan contoh persoalan TSP yang telah disebutkan diatas, berikut adalah langkah penyelesaiannya.
-
Dimulai dari simpul A, penyelesaian pada tahap ini adalah memilih sisi yang bersisian dengan simpul yang sedang diproses saat ini (sisi yang dipilih akan dimasukkan kedalam himpunan jalur untuk solusi) yang memiliki bobot sisi paling kecil. Setelah diketahui sisi dengan bobot terkecil, maka simpul yang dihubungkan oleh sisi itu menjadi simpul yang akan diproses selanjutnya.
-
Ulangi langkah 1 terhadap simpul yang telah dipilih pada langkah 1 hingga semua simpul telah dikunjungi dan harus kembali ke simpul A.
Untuk lebih mudah memahami, berikut adalah tabel yang merangkum keputusan yang diambil disetiap tahap (simpul).
| Simpul Sekarang | Simpul yang dipilih | Bobot total sementara |
|---|---|---|
| A | B | 20 |
| B | C | 50 |
| C | D | 62 |
| D | A | 97 |
Maka solusi dari persoalan dengan algortima greedy tersebut adalah jalur A>B>C>D>A dengan total bobot 97. Solusi ini sama optimal dengan solusi persoalan yang sama dengan algortima greedy, namun perlu dipahami sesungguhnya algoritma greedy tidak selalu memberikan solusi yang optimal. Tapi unutk kasus ini solusinya ‘kebetulan’ juga merupakan solusi yang paling optimal.
3. Algoritma Branch and Bound
Selain dengan kedua algoritma yang telah dijelaskan diatas, penyelesaian TSP juga dapat dilakukan dengan algoritma branch and bound. Algoritma branch and bound adalah algoritma yang merupakan perpaduan antara algoritma greedy dengan algoritma Breadth First Search(BFS). Proses penyelesaian dengan algoritma branch and bound biasanya dimodelkan dengan menggunakan pohon. Dengan simpul pohon menyimpan nilai sementara dan sisi pohon menunjukkan rute yang dipilih untuk dilewati dalam pencarian. Karakteristik dari penyelesaian dengan algoritma branch and bound ini adalah adanya bound yang menjadi pembatas antara solusi yang mungkin dengan solusi yang tidak mungkin. Jadi dalam perjalanan pencarian, jiaka suatu nilai sementara melebihi bound (bisa lebih kecil atau lebih besar, tergantung persoalan), maka pencarian pada rute itu akan dihentikan karena dpata dipastikan tidak akan menuju ke solusi. Dengan metode ini, kompleksitas algoritma untuk mnyelesaikna TSP ini dapat jauh diefisienkan dibandingkan dengan penyelesaian menggunakan algoritma brute force. selain itu hasil yang didapat juga pasti optimal, sebab algortima branch and bound ini dapat mencari semua kemungkinan solusi. Jika suatu solusi ditemukan, solusi tersebut akan menjadi nilai bound yang baru dan pencarian solusi akan dialnutkan hingga semua kemungkinan yang mengarah ke solusi sudah diperiksa seluruhnya. Dan apabila ditemukan solusi baru dengan nilai yang lebih optimal, solusi sebelumnya akan dibatalkan (dalam pemodelan dengan pohon, simpul solusi yang tidak optimal akan ‘dibunuh’). Diakhir pencarian, simpul daun dari pohon yang masih ‘hidup’ merupakan solusi dari persoalan.
Berikut adalah tahapan untuk menyelesaikan persoalan TSP dengan algoritma branch and bound. Untuk lebih mudahnya, akan digunakan contoh soal seperti pada penjelasan algoritma-algoritma sebelumnya.
-
Menentukan bound dan fungsi pembatas untuk bound
Fungsi pembatas adalah fungsi untuk menghitung apakah bobot sementara sudah melebihi bound atau belum. Dengan fungsi pembatas ini proses pencarian yang terindikasi tidak akan menemui solusi akan langsung dihentikan dan mencari alternatif solusi lain.
Untuk contoh persoalan TSP diatas, fungsi pembtas yang bisa digunakan adalah dengan menggunakan bobot tur lengkap. Pertama, menentukan bound. Nilai bound merupakan nilai terkecil dari seluruh kemungkinan sisi dari graf. Untuk menghubungkan setiap simpul, maka setiap simpul harus bersisian dengan 2 sisi. Maka untuk menghitung bobot tur lengkap, untuk setiap simpul, cari 2 sisi dengan bobot paling kecil, kemudian jumlahkan 2 sisi-sisi terkecil dari setiap simpul lalu hasilnya dibagi 2.
Simpul Dua sisi terkecil yang bersisian dengan simpul A AB dan AD B AB dan BC C BC dan CD D AD dan CD Maka nilai bobot tur lengkapnya adalah (AB+AD+AB+BC+BC+CD+AD+CD)/2 atau sama dengan 96,5. Nilai tersebut juga merupakan nilai bound.
Selanjutnya, untuk menghitung fungsi pembatas setiap memilih satu jalur baru, jalur tersebut harus diiikutkan dalam perhitungan meskipun bukan salah satu dari 2 sisi terkecil yang bersisian dengan simpul. Misal simpul sekarang adalah simpul A, dan jalur AC telah dipilih, makan simpul yang bersisian dengan simpul A unutk dihitung pada fungsi pembatas buakan AB dan AD, melainkan AB dan AC.
-
Bentuk pohon pencarian
Untuk membentuk pohon pencarian, akar dari pohon merupakan awal perjalanan yaitu dari simpul A dengan cost sama dengan bound yaitu 96,5. Selanjutnya,
-
Bangkitkan simpul dengan memilih setiap sisi yang bersisian dengan simpul akar, unutk setiap simpul yang dibangkitkan pada pohon keputusan, hitung kembali nilai fungsi pembatas dengan jalur yang telah dipilih sebagai cost dari simpul.
-
Pilih simpul anak anak pada langkah 1 dengan cost terkecil (cara greedy) kemudian lakukan langkah 1 pada simpul yang dipilih. Proses tersebut dilakukan hingga solusi ditemukan.
-
Jika salah sudah ditemukan satu solusi, solusi tersebut menjadi nilai bound baru. Kemudian, ‘bunuh’ semua simpul daun yang masih ‘hidup’ pada pohon pencarian solusi jika nilainya melebihi bound. Jika semua simpul daun terbunuh maka solusi tersebut merupakan solusi persoalan, jika masih ada simpul daun yang tidak terbunuh lakuakn pencaria pada simpul tersebut dimulai dari simpul daun dengan cost terkecil (mencari kemungkinan solusi lain).
Berikut adalah contoh pohon pencarian solusi yang dibentuk dari persoalan diatas.
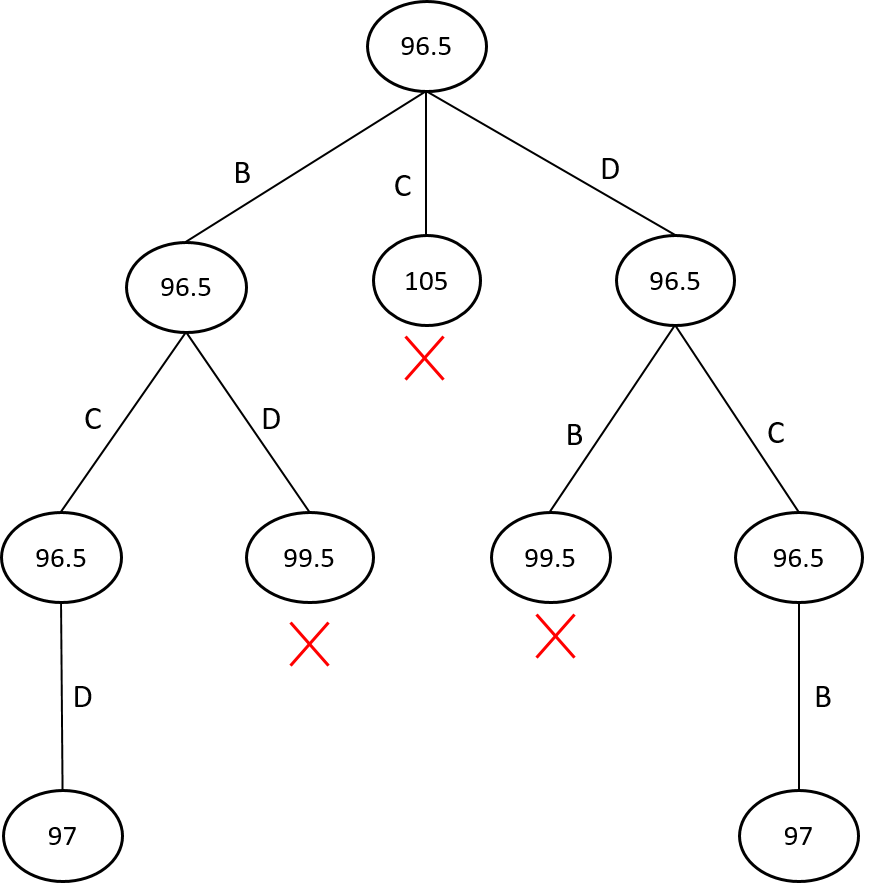
Dari gambar tersebut dapat dilihat bahwa jalur solusinya adalah jalur yang melewati simpul B>C>D dan D>C>B, maka jalur solusi dari persoalan diatas adalah A>B>C>D>A dan A>D>C>B>A dengan bobot total 97.
-
4. Dynamic Programming
Algoritma terakhir yang akan dibahas pada artikel kali ini adalah Dynamic Programming. Penyelesaian persoalan menggunakan *dynamic programming memiliki dua karakteristik.
-
Penyelesaian persoalan dipecah menjadi tahap-tahap (stage).
-
Solusi dari persoalan merupakan serangkaian keputusan yang saling berkaitan.
Berdasarkan karakteristik diatas, pengelesaian persoalan dengan dynamic programming dilakukan secara rekursif pada per tahapnya. sekilas penyelesaian dengan dynamic programming ini mirip dengan penyelesaian dengan algoritma greedy, namun kedua cara penyelesaian ini sesungguhnya berbeda. Pada algoritma greedy rangkaian keputusan yang dihasilkan sebagai penyelesaian persoalan hanya ada satu dan solusi yang dihasilkan belum tentu optimal, sementara pada dynamic programming ada banyak sehingga mempertimbangkan lebih banyak solusi untuk dipilih yang paling optimal.
Berikut adalah cara untuk menyelesaikan permasalah TSP dengan dynamic programming.
-
Tentukan fungsi rekursif, yaitu yang terdiri dari basis dan rekurens. Basis berisi jarak kota awal, dalam persoalan ini dalah kota A ke, ke seluruh kota disebelahnya. Sementara rekurens adalah jalur yang memiliki bobot total terkecil dari semua jalur yang mungkin dilewati dari awal ke simpul tersebut.
-
Lakukan penyelesaian per tahap hingga semua simpul telah diperiksa dan hasil dari persoalan telah diketahui.
-
Telusuri jalur yang yang menjadikan hasil optimal tersebut.
Referensi :
(1) Munir, Rinaldi. 2009. Diktat Kuliah IF2211 Strategi Algoritma. Bandung : Program Studi Teknik Informatika, Sekolah Teknik Elektro dan Informatika, Institut Teknologi Bandung.