Berbagai Algoritma Pemecahan Maximum-Flow Problem
Maximum-flow problem (Permasalahan Aliran Maksimum) merupakan salah satu model permasalahan yang sering digunakan dalam optimasi suatu sistem di dunia nyata sehingga sistem tersebut menghasilkan produksi semaksimal mungkin. Maximum-flow (aliran maksimum) suatu sistem ditinjau untuk mengetahui jumlah maksimum yang dapat dilalui oleh suatu aliran tertentu dari satu sumber ke suatu tampungan. Jumlah yang dialirkan dari sumber sama dengan jumlah yang berada pada tampungan. Maximum-flow problem digambarkan dalam suatu graf berarah dengan masing-masing sisi berperan sebagai arah aliran dan masing-masing sisi memiliki bobot. Ilustrasi singkat mengenai konsep maximum-flow problem akan dijelaskan di bawah ini.
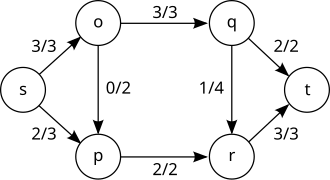
Gambar 1. Graf Berarah dan Berbobot
Graf di atas menunjukan aliran yang berasal dari suatu sumber (source) s ke penampungan (sink) t dengan melewati keempat simpul, yaitu o, p, q, dan r. Anggap sisi-sisi pada graf sebagai pipa. Setiap pipa memiliki bobot. Bobot tersebut menunjukan jumlah aliran (flow) yang telah melewati pipa dari sumber menuju penampungan, serta kapasitas maksimum aliran (capacity) yang dilewati oleh sebuah pipa. Kedua bobot tersebut dituliskan dengan cara jumlah aliran di sebelah kiri dan kapasitas dituliskan sebelah kanan, keduanya dibatasi dengan garis miring atau garis tegak.
Dari graf tersebut di atas, akan dicari aliram maksimum yang mungkin dari sumber S ke penampungan T dengan syarat sebagai berikut:
1. Jumlah aliran pada pipa tidak melebih jumlah kapasitas pipa
2. Jumlah aliran yang masuk dari dari satu simpul ke simpul lain sama.
Untuk mencari aliran maksimum pada graf tersebut bukanlah hal mudah. Harus diperhatikan bahwa setiap sisi memiliki kapasitas yang berbeda-beda, sedangkan jumlah aliran yang melewati pipa dari sumber ke penampungan haruslah sama sehingga aliran maksimum bukan hanya mengenai kapasitas satu sisi, melainkan memperhitungkan kapasitas banyak sisi. Selain itu, sebagian besar simpul berderajat lebih dari satu, artinya aliran mengalami percabangan sehingga perhitungannya menjadi lebih rumit.
Oleh karena itu, dibuatlah algoritma-algoritma yang dapat memecahkan permasalahan maximum-flow ini. Pada tulisan ini, akan dijelaskan lebih lanjut mengenai algoritma pemecahan maximum-flow problem. Algoritma yang akan dijabarkan pada tulisan kali ini adalah:
Algoritma Ford-Fulkerson
Salah satu algoritma paling terkenal adalah Algoritma Ford-Fulkerson. Algoritma ini memecahkan masalah dengan cara mencari lintasan dari sumber ke penampungan yang masih memiliki kapasitas untuk dilewati sehingga aliran bisa melewati lintasan tersebut dengan jumlah semaksimal mungkin.
Langkah-langkah dalam mengimplementasikan algoritma Ford-Fulkerson untuk mencari aliran maksimum adalah sebagai berikut:
- Menginisialisasi jumlah aliran dari sumber S ke penampungan T pada setiap sisi dengan 0.
- Mencari lintasan augmenting. Lintasan augmenting merupakan lintasan yang berasal dari simpul sumber menuju simpul penampungan. Lintasan augmenting terbagi menjadi dua, yakni lintasan dengan sisi selanjutnya belum penuh (non-full forward-edges), atau lintasan dengan sisi sebaliknya tidak kosong (non-empty backward-edge). Sisi belum penuh berarti jumlah aliran lebih kecil sama dengan kapasitas. Sisi tidak kosong berarti jumlah aliran lebih besar nol. Misalkan pada Gambar 1, lintasan s, o, q, t merupakan lintasan augmenting. Begitu juga dengan lintasan s, p, r, t. Perlu diperhatikan bahwa dalam pemilihan lintasan augmenting, penghitung yang satu dengan yang lain dapat menghasilkan lintasan augmenting yang berbeda-beda, namun aliran maksimum total yang didapat hasilnya akan sama.
- Selama masih ada lintasan augmenting, proses perhitungan terus berjalan. Perhitungan dilakukan berdasarkan kapasitas terkecil pada sisi dalam lintasan augmenting (bottleneck capacity). Jumlah aliran maksimum yang dapat dilalui suatu lintasan adalah kapasitas tersisa yang terkecil pada sisi dari lintasan tersebut. Kapasitas tersisa suatu sisi merupakan pengurangan dari kapasitas awal dengan jumlah aliran yang telah melewati sisi. Jumlah aliran maksimum suatu lintasan kemudian ditambahkan pada masing-masing jumlah aliran sisi yang terlibat pada lintasan tersebut.
- Langkah 1 dan 2 dilakukan sampai lintasan augmenting sudah tidak ada.
- Menjumlahkan semua jumlah aliran maksimum pada setiap lintasan augmenting. Maximum-flow suatu sistem merupakan total dari semua jumlah aliran maksimum pada setiap lintasan augmenting
Langkah algoritma tesebut pada pseucode dituliskan sebagai berikut:
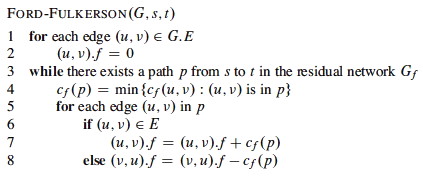
Gambar 2. Pseudocode Algoritma Ford-Fulkerson
Contoh pengimplementasian Algoritma Ford-Fulkerson pada pemecahan maximum-flow problem digambarkan pada ilustrasi di bawah ini.

Gambar 3. Contoh pengimplementasian Algoritma Ford-Fulkerson pada pemecahan maximum-flow problem
Algoritma Edmonds-Karp
Algoritma Edmonds-Karp merupakan penyempurnaan dari algoritma Ford-Fulkerson. Perbedaan mendasar dari kedua algoritma tersebut adalah pemilihan lintasan augmenting. Lintasan augmenting pada algoritma Ford-Fulkerson biasanya tidak ditentukan berdasarkan apapun asalkan terdapat non-full forward-edges dan non-empty backward-edge. Hal ini memungkinkan terjadi pemilihan lintasan augmenting yang kurang baik dan pemilihan-pemilihan selanjutnya akan terkena imbasnya sehingga menjadi kurang efisien.
Pada algoritma Edmonds-Karp, pemilihan lintasan augmenting berdasarkan jumlah sisi paling sedikit pada beberapa pilihan lintasan. Lintasan dengan jumlah sisi paling sedikit akan didahulukan. Jika terdapat beberapa lintasan dengan jumlah sisi yang sama, maka yang didahulukan adalah lintasan dengan simpul memiliki abjad atau urutan terkecil. Pemilihan lintasan augmenting algoritma Edmonds-Karp ini menggunakan algoritma Breadth-First Search (BFS). Setiap pilihan lintasan dimasukkan ke dalam antrian. Lintasan dengn jumlah sisi paling sedikit didahulukan dalam antrian.
Langkah yang digunakan pada algoritma Edmonds-Karp sama dengan langkah yang digunakan pada algoritma Edmonds-Karp. Perbedaannya hanyalah pada langkah pemilihan lintasan augmenting.
Langkah algoritma tesebut pada pseucode dituliskan sebagai berikut:
Edmonds-Karp(G,s,t)
1 for each edge (u, v) element of G.E
2 (u, v).f = 0
3 flow = 0; Gf = G
4 while there exists a path p from s to t in the residual graph Gf
5 Let p be an s - t path in Gf with the minimum number of edges
6 Augment flow using P
7 Update Gf
8 return flow
Algoritma Dinic
Algoritma Dinic merupakan algoritma pemecahan maximum-flow problem. Algoritma ini memanfaatkan konsep blocking flow dalam penentuan lintasan augmenting. Blocking flow pada suatu graf menyebabkan setidaknya memiliki satu sisi pada semua lintasan dari sumber ke penampungan yang jumlah alirannya sama dengan jumlah kapasitas maksimumnya (sisi tidak bisa dialiri lagi). Penjelasan mengenai penggunaan blocking flow akan dijelaskan lebih lanjut pada bagian langkah pengimplementasian algoritma Dinic di bawah ini.
Langkah-langkah dalam mengimplementasikan algoritma Dinic untuk mencari aliran maksimum adalah sebagai berikut:
- Menginisialisasi jumlah aliran dari sumber S ke penampungan T pada setiap sisi dengan 0.
- Mengonstruksi suatu graf residu relatif terhadap aliran yang ada. Graf residu merupakan graf yang menunjukan kapasitas ketika sudah ada suatu aliran yang mengalir di graf tersebut. Jika belum ada aliran yang mengalir, maka graf residu sama dengan graf awal (flow = 0).
- Membentuk lintasan augmenting dari graf residu. Jika tidak ada lintasan augmenting yang memenuhi (aturan penentuan lintasan augmenting sama dengan aturan pada algoritma Edmonds-Karp, yakni memilih lintasan dengan sisi tersedikit), maka keluarkan nilai flow yang telah didefinisikan sebelumnya. Jika terdapat lintasan augmenting yang memenuhi, maka blocking flow dibentuk. Dengan blocking flow, dapat dipastikan bahwa suatu lintasan augmenting memiliki sisi yang sudah penuh (jumlah aliran sisi sama dengan jumlah kapasitas maksimum sisi).
- Melakukan tahap 2 dan 3 sampai tidak terdapat lintasan augmenting yang memenuhi.
- Menjumlahkan semua jumlah aliran maksimum pada setiap lintasan augmenting. Maximum-flow suatu sistem merupakan total dari semua jumlah aliran maksimum pada setiap lintasan augmenting
Langkah algoritma tesebut pada pseucode dituliskan sebagai berikut:
Dinic(G,s,t)
1 for each edge (u, v) element of G.E
2 (u, v).f = 0
3 flow = 0; Gf = G
4 while there exists a path p from s to t in the residual graph Gf
5 find blocking flow of path p in Gf
6 cf(p) = blocking flow of path p in Gf
7 for each edge (u, v) in p
8 if (u, v) element of E
9 (u, v).f = (u, v).f + cf(p)
10 else (v, u).f = (v, u).f - cf(p)
11 flow = flow + cf(p)
12 Update Gf
13 return flow
Algoritma Push-Relabel
Algoritma push-relabel, berbeda dengan tiga algoritma di atas, tidak menggunakan konsep lintasan augmenting sama sekali. Algoritma ini menggunakan konsep aliran air, yakni kecenderungan air untuk mengalir dari tempat yang lebih tinggi ke tempat yang lebih rendah. Oleh karena itu, pada algoritma ini, terdapat properti yang disebut height (tinggi) pada masing-masing simpul pada graf, termasuk sumber dan tampungan. Pada algoritma ini, tidak hanya sisi atau pipa yang berperan, tetapi juga simpul atau tangki berperan juga. Selain height, properti yang dimiliki oleh simpul adalah excess flow. Excess flow merupakan jumlah aliran yang sedang ditampung oleh suatu tangki. Properti ini tidak dimiliki oleh simpul sumber.
Ada dua operasi utama pada algoritma ini, push dan relabel, sesuai dengan nama algoritma ini.Langkah-langkah dalam mengimplementasikan algoritma push-relabel untuk mencari aliran maksimum adalah sebagai berikut:
- Menginisialisasi jumlah aliran dari sumber S ke penampungan T pada setiap sisi dengan 0. Height pada setiap simpul juga diinisialisasi menjadi nol, kecuali pada simpul sumber. Height pada simpul sumber dinyatakan sebagai n. Kemudian, semua jumlah aliram pada sisi yang keluar dari simpul sumber dibuat penuh (jumlah aliran sisi sama dengan jumlah kapasitas maksimum). Aliran tersebut disebut pre-flow
- Push. Operasi ini dijalankan ketika terdapat sisi memiliki jumlah aliran sisi f(u,v) tidak sama dengan jumlah kapasitas maksimum sisi c(u,v), excess flow sisi awal e(u) lebih besar dari nol, dan tinggi simpul awal h(u) lebih besar dari tinggi simpul akhir h(v). Jumlah aliran kemudian didorong (push) ke simpul akhir adalah nilai paling kecil dari jumlah sisa kapasitas sisi cf(u),v (pengurangan dari jumlah kapasitas maksismum sisi dengan jumlah aliran sisi) dan excess flow simpul awal.
- Relabel. Operasi ini dijalankan ketika suatu tangki atau simpul memiliki excess flow lebih besar dari nol, namum tidak ada tangki tujuan yang memiliki height yang lebih rendah dari dirinya sehingga tangki tersebut tidak dapat mengalirkan aliran ke tangki lain. Height simpul ini kemudian dinaikkan menjadi satu kali lebih besar dari simpul akhir manapun yang dihubungkan oleh satu sisi yang sama. Oleh karena operasi relabel ini, operasi push mungkin untuk dijalankan.
- Melakukan kedua operasi push dan relabel sampai operasi tersebut tidak dapat dijalankan kembali. Menghitung jumlah total aliran maksimum pada sistem.
Syarat operasi push dapat dijalankan
f(u,v) tidak sama dengan c(u,v)
h(u) > h(v)
e(u) > 0
Nilai flow yang di-push
flow = min(e(u),f(u,v))
Syarat operasi relabel dapat dijalankan
h(u) <= h(v)
Langkah algoritma tesebut pada pseucode dituliskan sebagai berikut:
Push(u,v)
1 temp = min (e(u), cf(u,v))
2 f(u,v) = f(u,v) + temp
3 f(v,u) = - f(u,v)
4 e(u) = e(u) - temp
5 e(v) = e(v) + temp
6 cf(u,v) = c(u,v) - f(u,v)
7 cf(v,u) = c(v,u) - f(v,u)
Relabel(u)
1 set temp = -1
2 for i = 0 to number of vertex do
3 v = G(u,i)
4 if cf(u,i) > 0 then
5 if temp = -1 or temp > h(v)
6 temp = h(v)
7 h(u) = temp + 1
Push-Relabel(G,s,t)
1 initialize
2 while there is an operation that can be carried out
3 Select an operation and perform it
Demikian algoritma-algoritma pemecahan maximum-flow problem, yakni algoritma Fordk-Fulkerson, algoritma Edmonds-Karp, Algoritma Dinic, dan algoritma Push-Relabel. Semoga bermanfaat.